Žmonijos sukurti tyrimų zondai jau aplankė visas Saulės sistemos planetas, nuo Merkurijaus iki Neptūno, ir gausybę mažesnių kūnų – palydovus, asteroidus, kometas, nykštukines planetas. Keli zondai – „Voyager 1“ ir 2, greičiausiai ir „Pioneer 10“ ir 11 – jau netgi paliko Saulės sistemą. Kaip skraido erdvėlaiviai Saulės sistemoje?Žmonijos sukurti tyrimų zondai jau aplankė visas Saulės sistemos planetas, nuo Merkurijaus iki Neptūno, ir gausybę mažesnių kūnų – palydovus, asteroidus, kometas, nykštukines planetas. Keli zondai – „Voyager 1“ ir 2, greičiausiai ir „Pioneer 10“ ir 11 – jau netgi paliko Saulės sistemą. Šios kelionės įprastai trunka ilgai: „Cassini“ iki Saturno keliavo septynerius metus, „New Horizons“ iki Plutono – dešimt, o „Voyageriai“ ir „Pionieriai“ iki Saulės sistemos krašto – apie 40-50. Iš kitos pusės, ilgai trunka ir, atrodytų, daug artimesnės misijos: „BepiColombo“ į Merkurijų keliauja aštuonerius metus, panašiai ilgai Saulės link skrido „Parker Solar Probe“. Kodėl taip nutinka? Ir kaip apskritai skraido erdvėlaiviai Saulės sistemoje? Praeitame pažintiniame straipsnyje pasakojau apie orbitas aplink Žemę, o dabar kviečiu susipažinti su šiek tiek tolimesniu, bet vis dar aplinkiniu, kosmosu.
Šį pažintinį straipsnį parašiau, nes turiu daug rėmėjų „Contribee“ platformoje. Ačiū jums! Jei manote, kad mano tekstai verti reguliarios paramos, kviečiu prie jų prisidėti.
Pradėkime kelionę nuo kosmoso ribos. Šimto ar kelių šimtų kilometrų aukštyje, skrisdamas apskritimine orbita, erdvėlaivis juda kiek daugiau nei aštuonių km/s greičiu. Ką jam reikėtų padaryti, kad pasiektų Mėnulį? Priešingai nei ant Žemės paviršiaus ar netgi atmosferoje, nukreipti nosį taikinio link ir spausti akceleratoriaus pedalą nėra geriausias pasirinkimas. Turimas greitis niekur nepranyks, o norėdamas pasiekti Mėnulį, erdvėlaivis turės sunaudoti gausybę kuro. Daug geresnis manevras yra tiesiog pagreitėti ta pačia kryptimi, kuria jau judama. Padidėjus greičiui, erdvėlaivis ima tolti nuo Žemės – jo orbita tampa elipsinė. Tinkamai parinkus pagreitėjimą, galima pasiekti, kad tolimiausias elipsės taškas kaip tik sutaptų su Mėnulio orbita. Pasiekus jį ir nieko nedarant, erdvėlaivis vėl imtų artėti prie Žemės, nes ten būdamas juda per lėtai, kad išsilaikytų. Taigi reikia pagreitėti dar kartą, kad orbita vėl taptų apskritiminė. Štai Mėnulio orbita ir pasiekta.
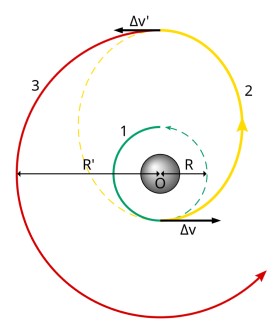 Hohmano perėjimo schema. Erdvėlaivis iš apskritiminės žalios orbitos per tarpinę elipsinę geltoną pereina į aukštesnę raudoną. Šaltinis: „Wikimedia Commons“ |
|---|
Aukščiau aprašytas manevras vadinamas Hohmano perėjimu. Konceptualiai jis yra ir paprasčiausias, nes reikalauja tik dviejų pagreitėjimų, nukreiptų tiesiai judėjimo kryptimi. Be to, dažniausiai jis yra ir efektyviausias pagal energijos sąnaudas. Skrydžiai į Marsą, pavyzdžiui, iš principo taip ir atliekami: erdvėlaivis pagreitinamas netoli Žemės, tada pusmetį ar kiek ilgiau skrieja iki Marso ir ten sulėtėja bei įeina į orbitą aplink planetą. Deja, manevras turi ir du esminius trūkumus. Pirmasis – kelionės trukmė: jei galėtume erdvėlaivio variklius laikyti įjungę visą laiką, iki Marso nuskristume per mažiau nei savaitę (plačiau tokią galimybę nagrinėjau čia). Bet varikliams reikia kuro, o tą kurą reikia gabentis kartu su savimi. Taigi norint išgauti didesnį greičio pokytį variklių darbu, reikalingas kuro kiekis auga eksponentiškai. Ši problema, vadinama „raketos lygties tironija“, kol kas neleidžia galvoti apie sparčius didelių erdvėlaivių skrydžius po Saulės sistemą. Iš kitos pusės, maži zondai gali bent jau teoriškai pasinaudoti Saulės burėmis (apie kurias irgi esu rašęs išsamiau).
Antroji Hohmano manevro problema – skrydžiai įmanomi tik specifiniais laiko intervalais. Jie vadinami „paleidimo langais“, nes atsidaro ir užsidaro priklausomai nuo planetų tarpusavio padėties. Štai Marsas ir Žemė į tinkamą konfigūraciją suskrenda maždaug kas 26 mėnesius. Kitu metu paleidę erdvėlaivį galėtume pasiekti Marso orbitą, tačiau būtume toli nuo pačios planetos, tad nuskristi iki jos reikėtų dar daugiau energijos, nei išnaudojome iš pradžių. Todėl įvairiausios misijos į Marsą išskrenda kas porą metų: „Curiosity“ 2011-ais, Indijos MOM ir NASA MAVEN 2013-ais, „ExoMars“ 2016-ais, „InSight“ 2018-ais, Emyratų bei Kinijos misijos ir „Perseverance“ 2020-ais ir taip toliau.
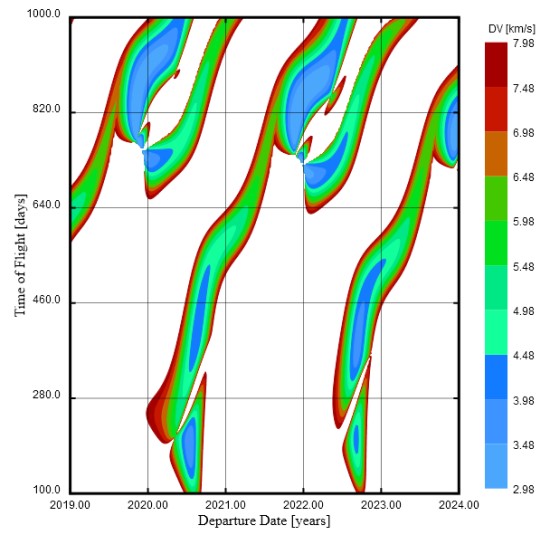
Skrydžio į Marsą trukmė ir energijos poreikis priklausomai nuo paleidimo laiko. Spalvoti regionai diagramos apačioje yra „paleidimo langai“, kai įmanomas skrydis, trunkantis trumpiau nei metus. Šaltinis: „Wikimedia Commons“
Skrydžiai į Venerą vyksta labai panašiai, kaip į Marsą. Tik čia reikia ne greitėti, o du kartus sulėtėti. Kelionė truktų šiek tiek trumpiau, apie 4-5 mėnesius. Paleidimo langai irgi atsiveria dažniau, maždaug kas 19-20 mėnesių. Turint omeny šiuos skaičius, gali pasirodyti keista, kodėl Venerai skiriama mažiau tyrimų dėmesio, nei Marsui, bet to priežastis – pragaištingos sąlygos planetos paviršiuje, kur bet koks mūsų zondas sugestų per kelias valandas.
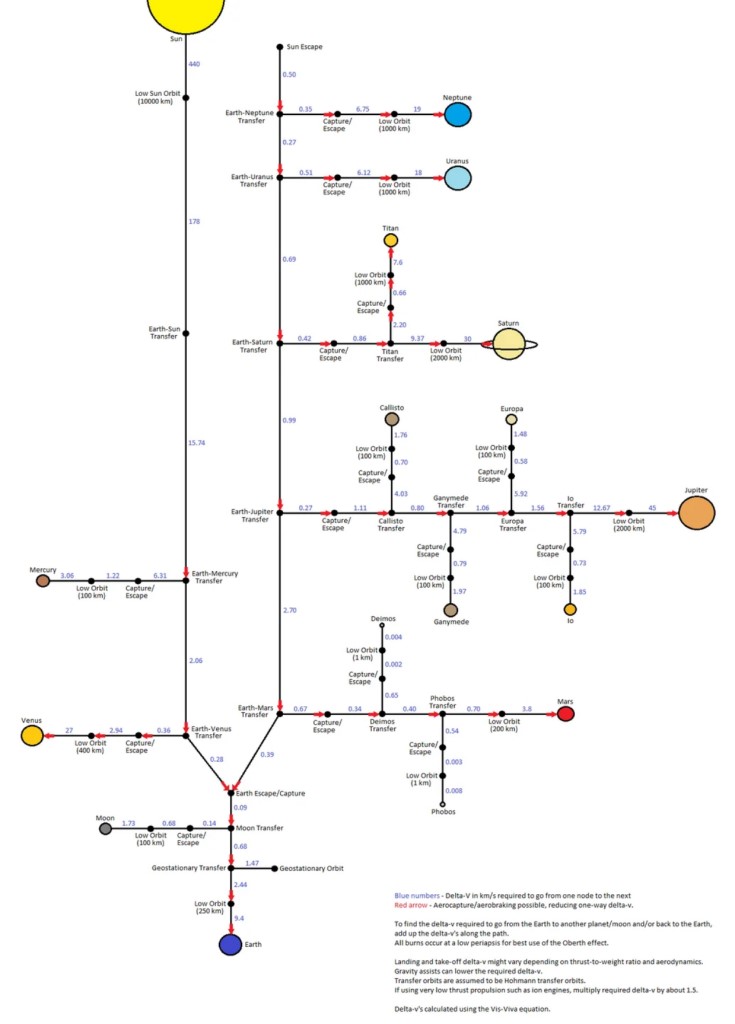
Skristi toliau – tiek tolyn nuo Saulės, tiek artyn prie jos – iš principo irgi galėtume Hohmano manevrais. Deja, energijos sąnaudos išauga labai stipriai. Jos dažnai nurodomos pagal bendrą greičio pokyčio poreikį, arba delta-V. Kelionei į Venerą ir į Marsą delta-V labai panašus, svyruoja tarp 4-5 km/s. Į Jupiterį galima nuskristi išleidus 5-6 km/s, į Saturną – apie 6,5 km/s. Skirtumai atrodo nedideli, bet nepamirškime, kad kuro sąnaudos auga eksponentiškai. O kelionei į Merkurijų delta-V išauga beveik iki 10 km/s; didžiąją dalį šio greičio pokyčio sunaudotume lėtėdami ties Merkurijumi. Tiesą sakant, šis poreikis yra netgi didesnis, nei reikalingas pabėgimui iš Saulės sistemos. Norėdami pasiekti Saulę, kuro turėtume sunaudoti dar gerokai daugiau, nei skrisdami iki Merkurijaus.
Taigi praktikoje Hohmano perėjimo orbitos tolimesniems skrydžiams nepakankamos. Laimei, egzistuoja energetiškai efektyvesnis būdas. Tai – gravitacinės svaidyklės efektas, kai erdvėlaivis pagreitėjimui pasinaudoja kitos planetos ar palydovo gravitaciniu lauku. Principas čia paprastas: erdvėlaivis priskrenda prie planetos iš vienos pusės, apskrieja aplink ją dalį lanko ir nuskrenda tolyn. Jei nejungia variklių, greitis planetos atžvilgiu tiek artėjant, tiek nutolstant kinta vienodai, pasikeičia tik jo kryptis. Tinkamai parinkus priartėjimo kryptį, Saulės atžvilgiu galima nemenkai pagreitėti – teoriškai kone dvigubai, praktikoje, aišku, kiek mažiau. Kadaise rašiau plačiau apie efekto matematiką.
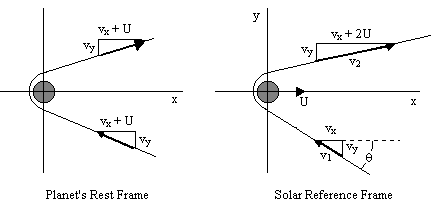
Gravitacinės svaidyklės schema. Kairėje – vaizdas iš planetos požiūrio taško: erdvėlaivis priskrenda ir nutolsta vienodu greičiu. Dešinėje – vaizdas iš Saulės požiūrio taško, kai planeta juda greičiu U į dešinę. Palydovo greitis gali reikšmingai išaugti (arba, priešingai, sumažėti), parinkus tinkamą priartėjimo kryptį. Šaltinis: mathpages
Gravitacinė svaidyklė tampa dar efektyvesnė, kai apjungiama su variklių darbu. Artėdamas prie planetos erdvėlaivis pagreitėja, toldamas – sulėtėja. Įjungtas variklis greitį didina tiesiškai: kuo ilgiau dirba, tuo daugiau greičio prideda (aišku, tam geriausia nukreipti variklį išilgai skridimo krypties, kaip ir Hohmano perėjimo atveju). O štai padidėjimas ir sumažėjimas yra „kvadratiški“, mat čia svarbu energijos tvermė, o kinetinė energija proporcinga greičio kvadratui. Taigi norint padidinti erdvėlaivio energiją, greitį geriausia didinti tada, kai erdvėlaivis juda didžiausiu greičiu – arčiausiai planetos. Toks manevras vadinamas Obertho efektu. Jis gali būti naudingas tiek skriejant pro planetą dideliu greičiu, tiek ir kelionės pradžioje, net kaip Hohmano perėjimo manevro dalis: užuot visą reikalingą pagreitėjimą padaręs vienu ypu, erdvėlaivis gali variklius įjungti trumpam, tada išjungti ir vėl įjungti apskriejęs pilną ratą. Tai naudinga, jei varikliai nėra galingi ir pilnas pagreitėjimas užtruktų ilgai; tuomet geriau jį sudalinti į laikotarpius, kai erdvėlaivis yra arčiausiai planetos.
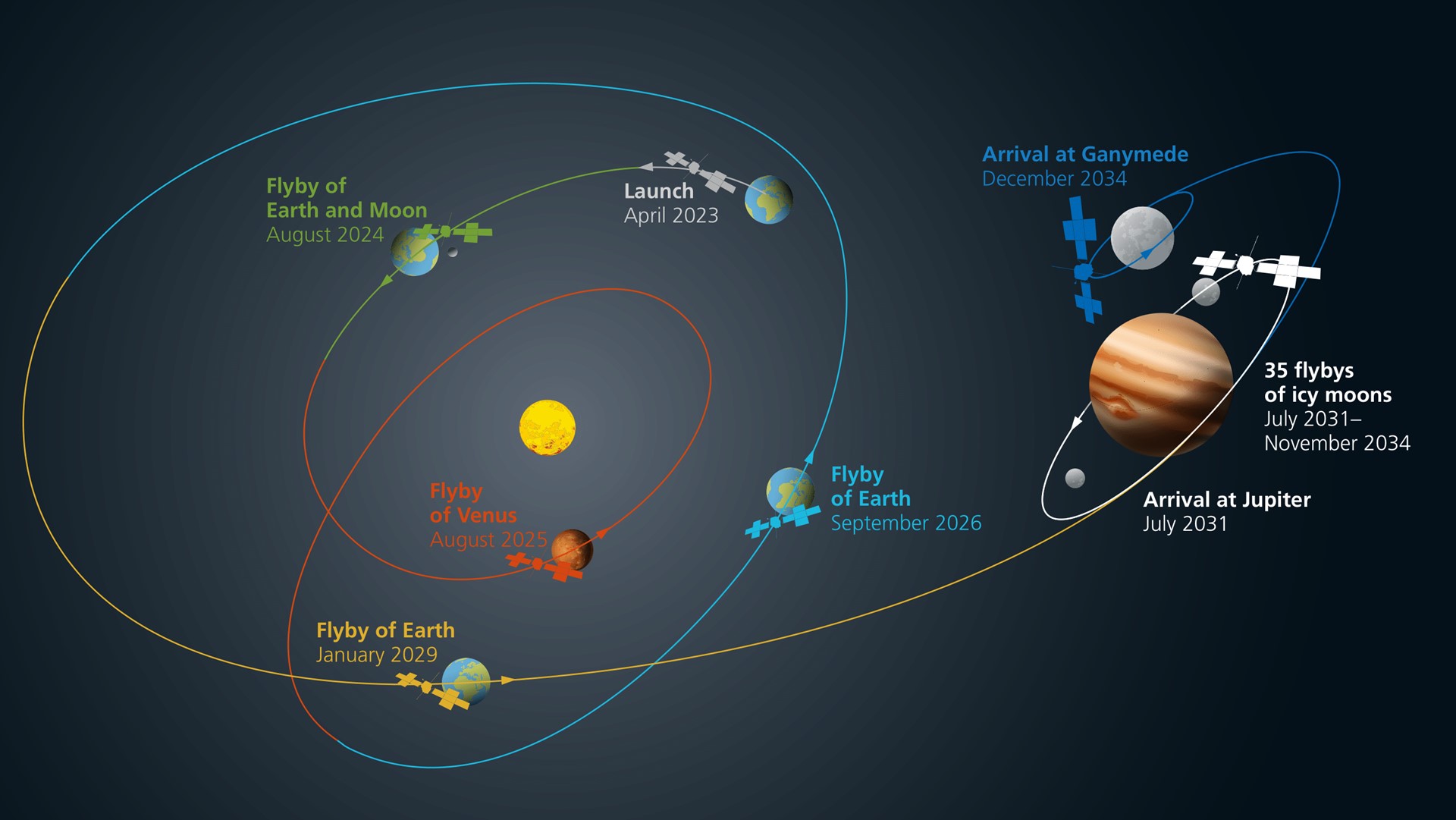
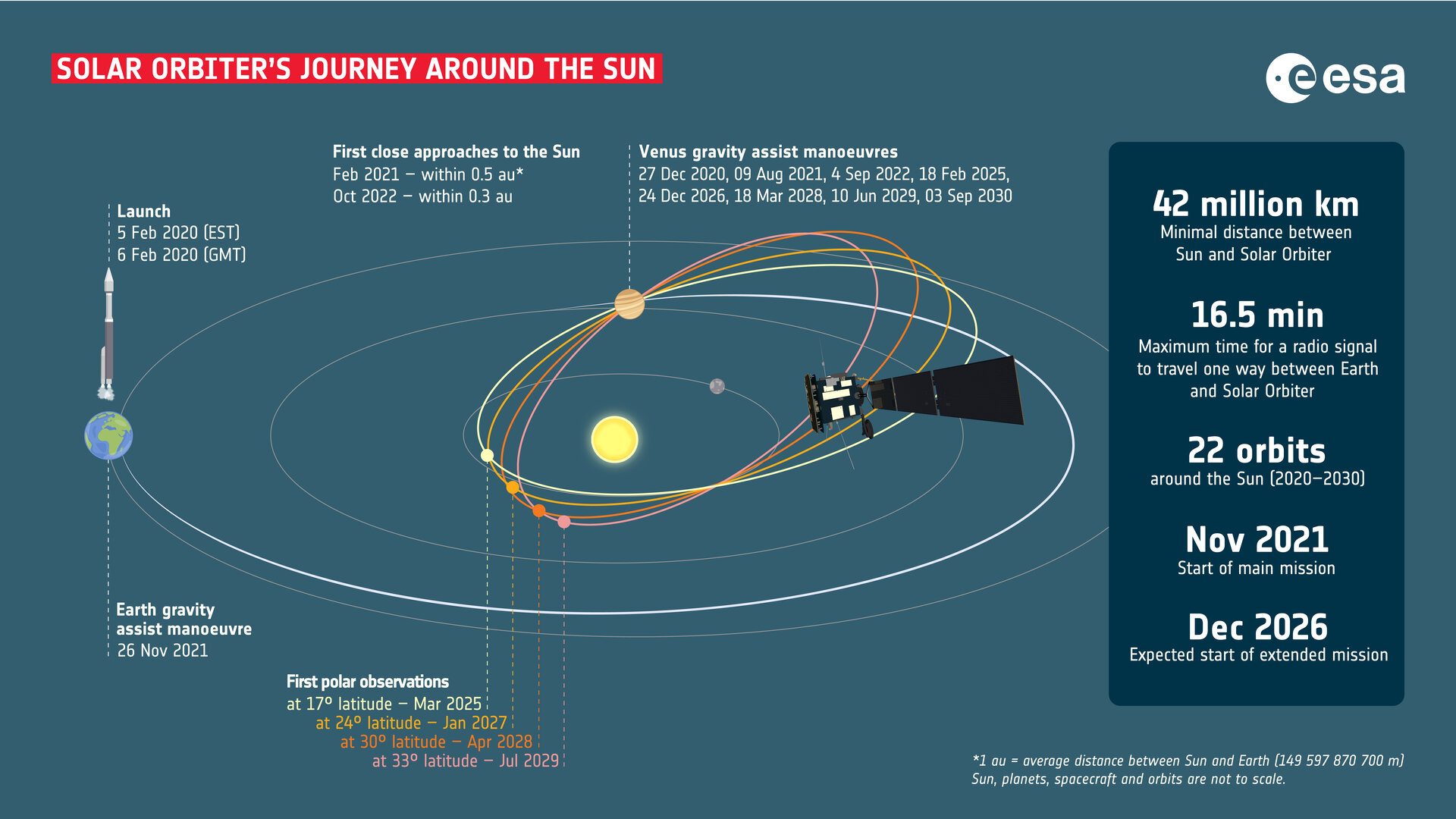
Gravitacines svaidykles naudojo ir tebenaudoja įvairūs mūsų zondai. Pavyzdžiui, New Horizons praskriejo šalia Jupiterio ir taip pagreitėjo maždaug 4 km/s. Jupiterio palydovus tirsiantis zondas JUICE, išskridęs užpernai balandį, pernai rugpjūtį praskrido pro Žemę ir pagreitėjo, šiemet pralėkė Venerą, 2026 ir 2029 metais vėl praskris pro Žemę ir tik tada pasileis Jupiterio link. Net visai artimi skrydžiai – į Mėnulį – dažnai pasinaudoja Obertho efektu ir orbitą pakelia, o prie Mėnulio – pažemina – per kelis manevrus. Parker „Solar Probe“ ir „Solar Orbiter“, du Saulės tyrimų zondai, ne kartą praskriejo pro Venerą, taip pakoreguodami savo trajektoriją. Pirmajam tai leido priskrieti beprecedentiškai arti prie Saulės, antrajam – pakilti iš ekliptikos plokštumos į palinkusią, kad galėtų stebėti Saulės ašigalius.
Tokie manevrai visada gerokai padidina kelionės trukmę, lyginant su skrydžiu tiesiai, tačiau sumažina kuro sąnaudas, nes dalį pagreitėjimo suteikia planetų gravitacija. Kol skraido robotiniai zondai, toks balansas dažniausiai yra naudingas; deja, žmonių kelionėms juo pasinaudoti (beveik) nebus įmanoma, nes tada kaip tik daug svarbiau bus nuvykti į tikslą kuo greičiau.
Vienas iš gravitacinės svaidyklės panaudojimo pavyzdžių, kurį paminėjau aukščiau, buvo „Solar Orbiter“ ir jo skrydis tolyn nuo ekliptikos. Ekliptika vadinama Žemės orbitos aplink Saulę plokštuma. Kitų septynių planetų orbitų plokštumos labai panašios. Taigi dažnai skrydžius, bent jau tarp planetų, galima planuoti beveik dviejuose matmenyse. Visgi kartais norisi, arba reikia, nutolti ir statmena kryptimi. Tam nepakanka greitėti ar lėtėti ta pačia kryptimi, kuria judama, todėl manevrai tampa mažiau efektyvūs ir energijos reikia daug daugiau. Gravitacinė svaidyklė tampa be galo svarbi: santykinai nedidelis kurso pokytis, artėjant prie planetos, gali visiškai pakeisti kryptį, kuria planeta pakreips palydovo trajektoriją. Būtent tuo „Solar Orbiter“ ir naudojosi, ir naudosis toliau, kol galiausiai jo orbita pasisuks maždaug 30 laipsnių į ekliptikos plokštumą.
Skrydžiai Saulės sistemoje – konceptualiai gana paprastas uždavinys. Tereikia žinoti, kur nori nuskristi, ir kokius kitus dangaus kūnus galima aplankyti. Žinoma, įvertinus tai, kad viskas nuolatos juda, ir kad net nedidelės paklaidos atliekant manevrą gali labai stipriai pakeisti, kur erdvėlaivis atsidurs po keleto metų, akivaizdu, kad skaičiavimų reikia labai tikslių. Ir visgi skrydžiai – tiek artyn prie Saulės, tiek ypač tolyn nuo jos – trunka ne vienus metus, mat kosmoso yra daug, o žmonijos galimybės įveikti milžiniškus atstumus kol kas – labai ribotos. Dar labiau neaprėpiama kosmoso platybė pasimato, kai pradedame kalbėti apie dar tolimesnius skrydžius ir bandymus pasiekti kitas žvaigždes. Apie juos irgi esu rašęs.
